Why is 45 a prime number?

Prime numbers are an essential concept in mathematics, and they play a crucial role in number theory. One such prime number is 45.

45 is a composite number that is divisible by factors other than 1 and itself. So, why is it considered a prime number? To understand this, let's examine its factors.

When we factorize 45, we find that it can be expressed as the product of 3 and 15. Both 3 and 15 are factors of 45. Additionally, 3 can be further factorized into 1 and 3, and 15 can be factorized into 3 and 5. Therefore, we can conclude that 45 can be expressed as the product of 3, 3, and 5.

Now, let's think about the definition of prime numbers. A prime number is a number that is only divisible by 1 and itself. Since 45 has additional factors besides 1 and itself, it cannot fulfill the definition of a prime number.

Therefore, although 45 may appear to be a prime number initially, a closer analysis reveals that it is, in fact, a composite number with factors other than 1 and itself.

In conclusion, despite its initial appearance, 45 is not a prime number. It is a composite number that can be factored into 3, 3, and 5.

What factors of 45 are prime?

When it comes to analyzing the factors of a number like 45, it is essential to determine which of these factors are prime numbers.

Prime numbers are those integers greater than 1 that can only be divided evenly by 1 and themselves. In the case of 45, its factors include 1, 3, 5, 9, 15, and 45.

Let's examine each factor of 45 to identify which are prime numbers.

Starting with the number 1, it is not a prime number because it can only be divided by 1 itself.

Next, we have the factor 3. This is indeed a prime number since it can only be divided by 1 and 3 without any remainder.

Following that, we come across the factor 5. Similar to 3, it is also a prime number since it can solely be divided evenly by 1 and 5.

Now let's move on to the factor 9. Unfortunately, it is not a prime number as it can evenly be divided by 1, 3, and 9.

The next factor on the list is 15. Like 9, it is not a prime number because it can be divided evenly by 1, 3, 5, and 15.

Finally, we reach the last factor of 45, which is the number 45 itself. It is not a prime number as it can be divided by 1, 3, 5, 9, 15, and 45.

In summary, out of the factors of 45, the prime numbers are 3 and 5. These are the only factors that can only be divided by 1 and themselves. The remaining factors, including 1, 9, 15, and 45, are not prime numbers as they have additional divisors.

Does 45 have exactly 2 factors?

When determining whether a number has exactly 2 factors, it is important to understand what factors are. Factors are whole numbers that divide evenly into a given number. In the case of 45, it is necessary to find all the numbers that divide evenly into it and see if there are exactly 2 factors.

First, let's identify the factors of 45. The number 45 can be divided evenly by 1, 3, 5, 9, 15, and 45 itself. These are the numbers that, when multiplied together, result in 45. Now, we need to count how many factors there are.

Out of the factors identified, we can see that there are 6 factors for the number 45. This means that 45 does not have exactly 2 factors.

In conclusion, the number 45 has more than 2 factors, making the statement "Does 45 have exactly 2 factors?" false. It is important to recognize that not all numbers have only 2 factors, and in the case of 45, it has 6 factors.

How do you know if a number is prime?

Prime numbers are integers that are divisible only by 1 and themselves. So, how can we determine if a given number is prime?

One way to check if a number is prime is by using the trial division method. This method involves dividing the number by all integers starting from 2 up to the square root of the number, and checking if any of these divisions result in a remainder of 0.

If we find a divisor that evenly divides the number, then it is not prime. However, if we reach the square root of the number without finding any divisors, then the number is prime.

For example, let's take the number 17. We divide it by 2, 3, 4, 5, and 6. None of these divisions yield a remainder of 0. Then we continue dividing it by 7, 8, and 9 until we reach the square root of 17, which is a little over 4. Since we haven't found any divisors, we can conclude that 17 is a prime number.

Another method to determine if a number is prime is using the Sieve of Eratosthenes. This method is efficient for finding prime numbers up to a certain limit. It involves creating a list of consecutive integers starting from 2 up to the limit. Then, we sequentially mark each multiple of the prime numbers found, starting from 2, as not prime.

Let's demonstrate with an example. If we want to find all the prime numbers up to 20, we start by marking 2 as prime and cross out all of its multiples (4, 6, 8, 10, 12, 14, 16, 18, and 20). Then, we move to the next unmarked number, which is 3, and cross out its multiples (6, 9, 12, 15, 18). We continue this process until we reach the square root of the limit. The remaining unmarked numbers are prime.

So, whether you use the trial division method or the Sieve of Eratosthenes, you can determine if a number is prime by following these techniques. It is important to note that prime numbers play a crucial role in various mathematical and cryptographic applications.

What is the factor tree for 45?

When we talk about the factor tree for a number, we are referring to a diagram that helps us understand its prime factors. Let's find out the factor tree for 45.

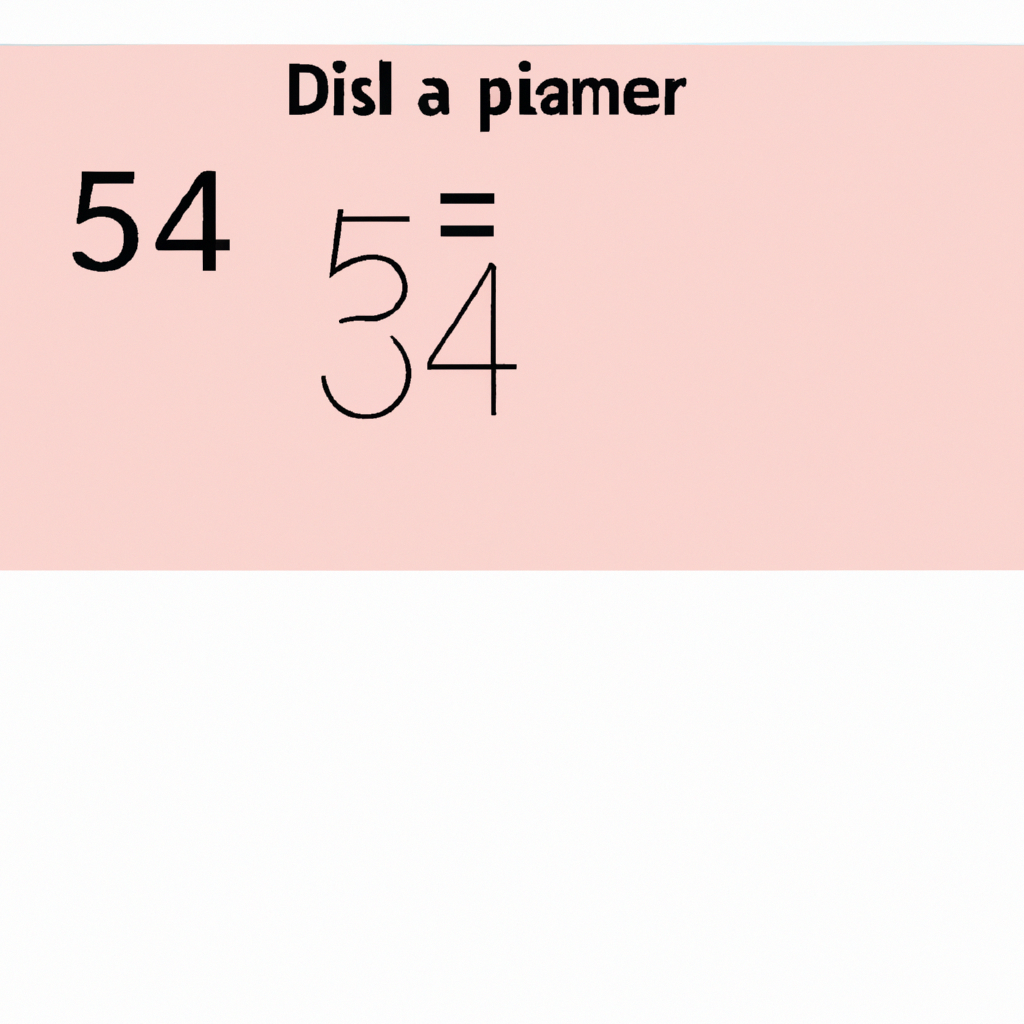
First, we start by finding any two numbers that multiply to give us 45. In this case, we have 5 and 9 as factors of 45. We can write it as 5 × 9 = 45.

Now, let's break down 5 and 9 further. 5 is a prime number, so we cannot break it down any further. However, 9 is not a prime number, so we can break it down into its factors. In this case, 9 can be written as 3 × 3.

Therefore, we can represent the factor tree for 45 as follows:

In summary, the factor tree for 45 shows that 45 can be broken down into the prime factors 5, 3, and 3. It helps us visualize the prime factors and their relationships to each other in a clear and organized manner.